Speed-Torque Characteristics of DC Shunt Motor
The speed-torque characteristics of DC shunt motor are also known as mechanical characteristics. They can be obtained from torque-current and speed-current characteristics of DC shunt motor.
The expression for back e.m.f in a DC motor is given by,
\[{{E}_{b}}={{k}_{a}}\phi N\text{ }\left[ {{k}_{a}}=\frac{ZP}{60A} \right]…(1)\]
Also, we have,
\[{{E}_{b}}=V-{{I}_{a}}{{R}_{a}}…(2)\]
On equating equations (1) and (2), we get,
\[{{k}_{a}}\phi N=V-{{I}_{a}}{{R}_{a}}\]
\[N=\frac{1}{{{k}_{a}}\phi }\left[ V-{{I}_{a}}{{R}_{a}} \right]…(3)\]
The expression for torque of a DC motor is given by,
\[T={{k}_{a}}\phi {{I}_{a}}\]
\[{{I}_{a}}=\frac{T}{{{k}_{a}}\phi }\]
Substituting the above value of Ia in equation (3), we get,
\[N=\frac{1}{{{k}_{a}}\phi }\left[ V-\left( \frac{T}{{{k}_{a}}\phi } \right){{R}_{a}} \right]\]
\[N=\frac{V}{{{k}_{a}}\phi }-\frac{T{{R}_{a}}}{{{({{k}_{a}}\phi )}^{2}}}…(4)\]
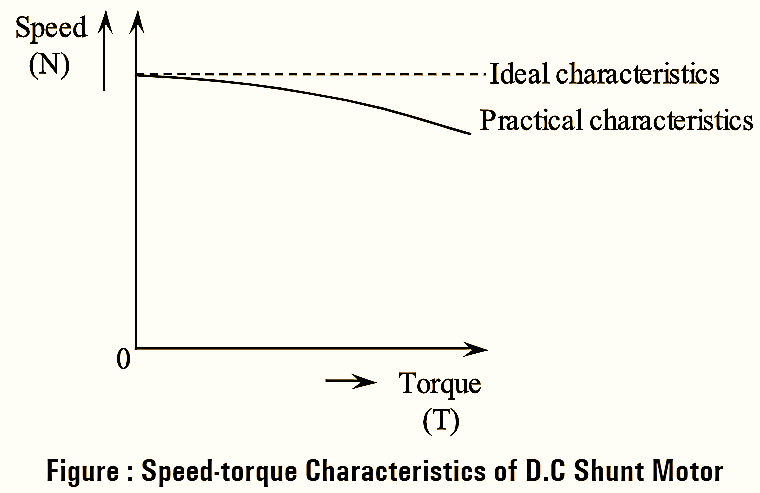
As the torque in a DC motor increases, flux (ϕ) decreases. This is because when torque is increased, armature current increases resulting in reduction of air gap flux ϕ i.e., due to armature reaction and saturation. Therefore, for increased torque there is an increase in the value \(\frac{T}{{{\phi }^{2}}}\) of equation (4) causing a drop in the speed of the motor. However, when the effect of armature reaction is neglected, the value of flux (ϕ) remains constant due to which for increase in torque there will not be much drop in speed of the DC shunt motor. The speed-torque characteristics of a DC shunt motor are drawn as shown below. Dotted line in above figure represents the ideal speed- torque characteristics of a DC shunt motor. But, due to the reduction in flux caused by the armature reaction, the curve is obtained as shown by the thick line.
Speed-Torque Characteristics of DC Series Motor
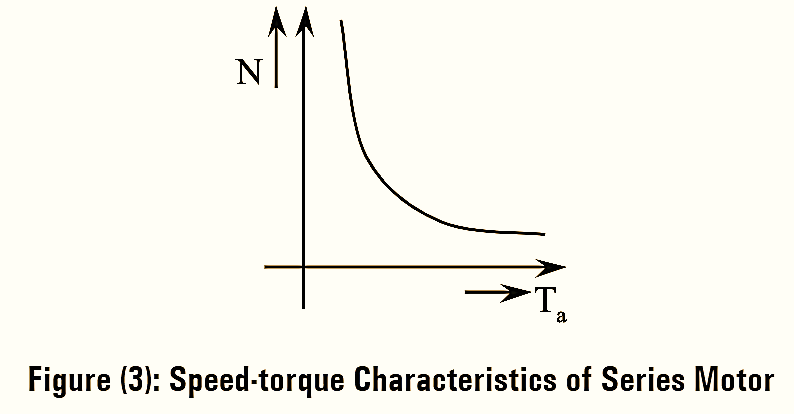
The speed-torque characteristics of DC series motor can be obtained or derived from the torque-current and speed-current characteristics of DC series motor. Therefore, armature torque and speed has inverse relationship as shown in figure (3).
We know that,
\[N\propto \frac{{{E}_{b}}}{\phi }\propto \frac{{{E}_{b}}}{{{I}_{a}}}\]
Since on no-load the speed is dangerously high, the series motors are never started on no-load. When the motor is connected across supply mains without load, the current drawn is small and hence ϕ is small and the speed tends to increase \(\left[ N\propto \frac{{{E}_{b}}}{\phi } \right]\). With increase in speed, Eb increases \(\left[ {{E}_{b}}=\frac{\phi ZN}{60}\times \frac{P}{A} \right]\) thus the field current decreases \(\left[ {{I}_{a}}=\frac{V-{{E}_{b}}}{{{R}_{a}}} \right]\) which in tum leads to decrease in flux and hence speed increases gradually. This process continues until the armature gets damaged. Hence, series motors are not suitable for the services where the load may be entirely removed.