
Working Principle of Ultrasonic Flow Meter
The velocity of propagation of ultrasonic sound waves in fluid changes when the velocity of the flow of fluid changes.
Working & Construction of Ultrasonic Flow Meter
The arrangement of flow rate measurement using ultrasonic transducer contains two piezoelectric crystals placed in the fluid (gas or liquid) whose flow rate is to be measured. Of these two crystals, one acts as a transmitting transducer (transmitter, T) and the other acts as a receiving transducer (receiver, R). The transmitter and thevreceiver are separated by some distance, say d. Generally, the transmitting transducer is placed in the up stream and it transmits ultrasonic pulses when an electronic oscillator energizes it. These ultrasonic pulses are then received by the receiving transducer placed at the downstream flow.
Let the time taken by the ultrasonic pulses to travel from transmitter and received at the receiver is Δt. If the direction of propagation of the signal is same as the direction of flow then the transit time can be given by,
\[\Delta {{t}_{1}}=\frac{d}{{{V}_{s}}+{{V}_{f}}}\]
Where,
d = Distance between two crystals (i.e., transmitter and receiver).
Vs = Velocity of propagation of ultrasonic sound waves in the fluid.
Vf = Linear velocity of flow.
If the direction of the signal is opposite with the direction of flow then the transit time is given by,
\[\Delta {{t}_{2}}=\frac{d}{{{V}_{s}}+{{V}_{f}}}\]
The signal traveling in the same direction of flow is sinusoidal in nature having f Hz frequency has a phase shift of,
\[\Delta {{\phi }_{1}}=\frac{2\pi fd}{{{V}_{s}}+{{V}_{f}}}\text{ rad}\]
Similarly, the sinusoidal signal traveling in the opposite direction of flow has a phase shift of,
\[\Delta {{\phi }_{2}}=\frac{2\pi fd}{{{V}_{s}}-{{V}_{f}}}\]
Now the determination of transit time or phase shift gives the velocity of fluid flow. Using this ultrasonic flow meter the flow rate can be determined in two methods. One method involves the measurement of difference in transit time (Known as transit time difference method) and the other method involves the measurement of difference in frequency (Known as oscillating loop system).
The output of oscillator which is a sinusoidal signal of 100 kHz frequency is supplied to the transmitter which transmits these signals to the receiver. With the help of commutating switch the functions of both transmitter and receiver are reversed.
Therefore, the difference that exists in the transit time can be given by,
\[\Delta t=\Delta {{t}_{2}}-\Delta {{t}_{1}}\]
\[\Delta t=\frac{d}{{{V}_{s}}-{{V}_{f}}}-\frac{d}{{{V}_{s}}+{{V}_{f}}}\]
\[\Delta t=\frac{2dv}{V_{s}^{2}-V_{f}^{2}}\]
This difference in transit time can be determined using a phase sensitive detector, driven in synchronization with the commutator. Generally the flow velocity inside the pipe is very low and can be neglected. Therefore the difference in transit time becomes,
\[\Delta t\approx \frac{2dv}{V_{s}^{2}}\]
Thus, the Δt is linearly proportional to velocity of flow.
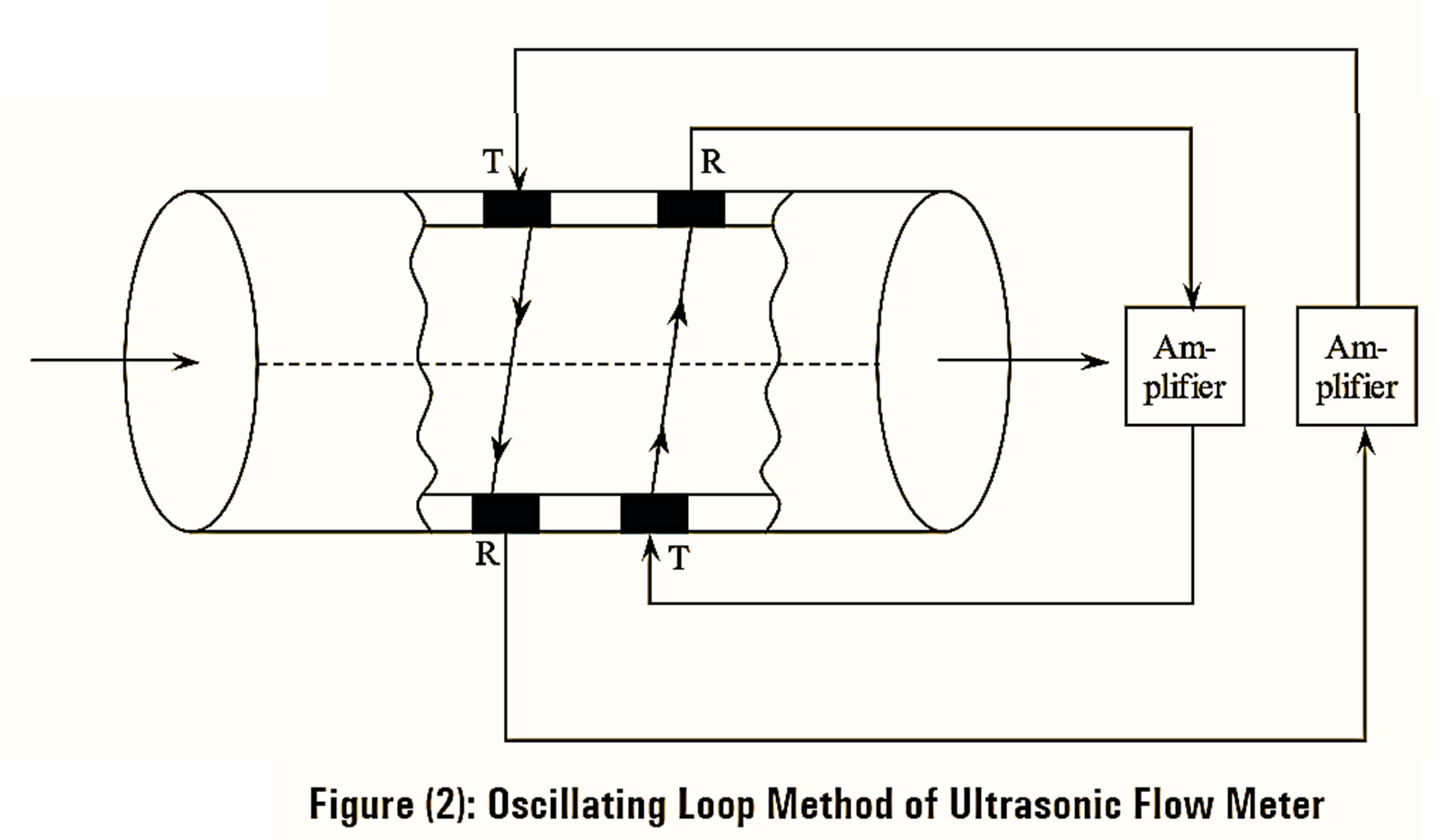
Another method of flow rate measurement using ultrasonic flow meter is shown in figure (2). This arrangement of flow rate measurement is based on frequency. It uses two self excited oscillating system in order to utilize the received pulses to trigger the transmitted pulses in feedback mechanism.
This helps to generate a train of pulses. The pulse repetition frequency for transmitter placed at upstream or in the forward propagating loop is given by,
\[{{f}_{1}}=\frac{1}{\Delta {{t}_{1}}}=\frac{1}{\frac{d}{({{V}_{s}}+{{V}_{f}}\cos \theta )}}=\frac{({{V}_{s}}+{{V}_{f}}\cos \theta )}{d}\]
Similarly, the pulse repetition frequency for transmitter placed at downstream or in the backward propagating loop is given by,
\[{{f}_{2}}=\frac{1}{\Delta {{t}_{2}}}=\frac{1}{\frac{d}{({{V}_{s}}-{{V}_{f}}\cos \theta )}}=\frac{({{V}_{s}}-{{V}_{f}}\cos \theta )}{d}\]
Therefore, the difference in these two frequencies is given by,
\[f={{f}_{1}}-{{f}_{2}}\]
\[f=\frac{({{V}_{s}}+{{V}_{f}}\cos \theta )}{d}-\frac{({{V}_{s}}-{{V}_{f}}\cos \theta )}{d}=\frac{2{{V}_{f}}\cos \theta }{d}\]
This frequency difference gives the flow rate of the fluid.
Advantages of Ultrasonic Flow Meter
- Not required any obstruction to the flow.
- It is not affected by changes in density, viscosity, and temperature.
- The output is linearly proportional to the input.
- Effectively used in bidirectional flow measurements.
- High accuracy and also has an excellent dynamic response.
Disadvantages of Ultrasonic Flow Meter
- The circuit arrangement is difficult.
- The cost of the arrangement is high.