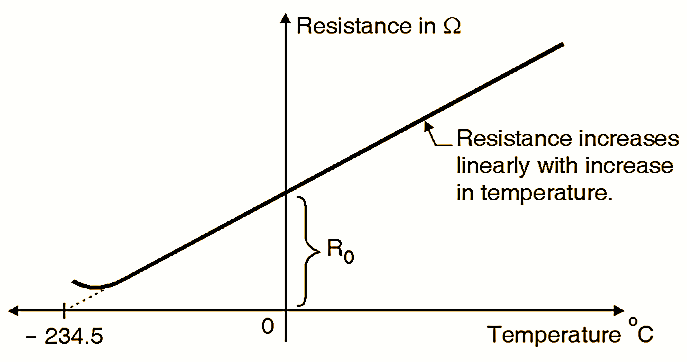
Figure 1.
For pure metals, the resistance increases linearly with increase in temperature as shown in Fig. 1.8.2, and for a certain range of temperature (typically 0 to 100ºC) the rate of increase of resistance (slope of the line) remains constant. The resistance of metals reduces with reduction in temperature and it reduces to 0 Ω at a temperature of -234.5ºC as shown in Fig. 1.
Resistance Temperature Coefficient (R.T.C.):
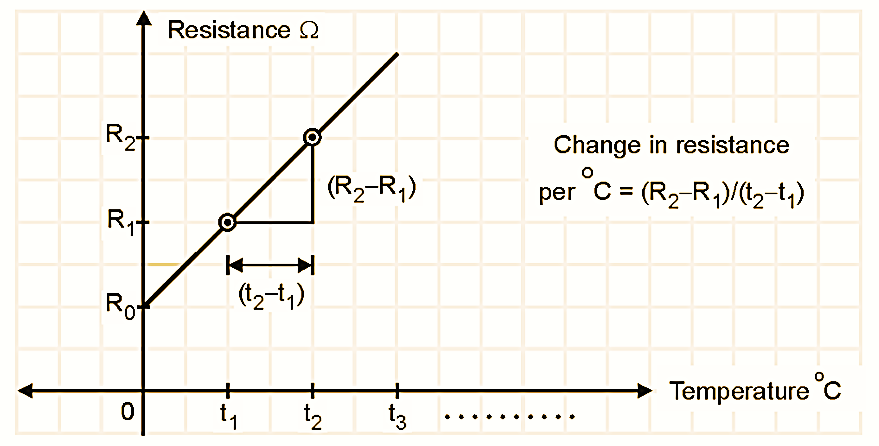
Figure 2.
Consider a conductor having an increasing resistance linearly with temperature as shown in Fig. 2.
Let,
R0 – Resistance at 0ºC
R1 – Resistance at t1ºC
R2 – Resistance at t2ºC
Definition :
The resistance temperature coefficient (RTC) at tºC is defined as the ratio of change in resistance of the material per degree Celsius to its resistance at tºC.
It is denoted by αt and its units are per degree Celsius (/ºC).
\[\text{RTC at t}{}^\circ \text{C = }{{\alpha }_{t}}=\frac{\text{ }\!\!\Delta\!\!\text{ R per }\!\!{}^\circ\!\!\text{ C}}{{{\text{R}}_{\text{t}}}}\]
Where,
ΔR – Change in resistance
Rt – Resistance at tºC
R.T.C. at 0ºC :
The R.T.C. at 0ºC is denoted by α0 and it is defined as follows :
\[{{\alpha }_{0}}=\frac{\text{Change in resistence per }\!\!{}^\circ\!\!\text{ C}}{\text{Resistence at 0 }\!\!{}^\circ\!\!\text{ C}}\]
The change in resistance per ºC is equal to the slope of the characteristics shown in Fig. 1.9.1.
α0 = Slope of the characteristic/R0
\[{{\alpha }_{0}}=\frac{({{R}_{2}}-{{R}_{1}})/({{t}_{2}}-{{t}_{1}})}{{{R}_{0}}}\]
R.T.C. at t1ºC :
The R.T.C. at t1ºC is denoted by α1 and it is defined as follows :
\[{{\alpha }_{1}}=\frac{\text{Change in resistance per }{}^\circ \text{C}}{\text{Resistance at }{{\text{t}}_{\text{1}}}{}^\circ \text{C}}\]
\[=\frac{\text{Slope}}{{{\text{R}}_{\text{1}}}}\]
\[{{\alpha }_{1}}=\frac{({{R}_{2}}-{{R}_{1}})/({{t}_{2}}-{{t}_{1}})}{{{R}_{1}}}\]
So in general we can write that the R.T.C. at temperature tn is given by,
\[{{\alpha }_{n}}=\frac{\text{Slope of the characteristics}}{{{\text{R}}_{\text{n}}}}\]
Where,
Rn = Resistance of the conductor at temperature Tn.
Unit of R.T.C.
We know that,
\[{{\alpha }_{n}}=\frac{\text{Slope of the charecteristics}}{\text{Resistance at }{{\text{t}}_{\text{1}}}{}^\circ \text{C}}\]
\[=\frac{({{R}_{2}}-{{R}_{1}})/({{t}_{2}}-{{t}_{1}})}{{{R}_{n}}}\]
\[=\frac{\Omega /{}^\circ \text{C}}{\Omega }=/{}^\circ \text{C}\]
Thus the R.T.C. is measured in per degree Celsius (/ºC).
Expression for Resistance at tºC
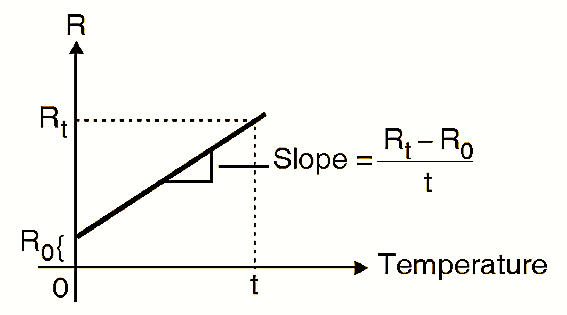
Figure 3.
Consider the R versus temperature characteristics of metal. (Fig. 3).
Let Rt be the value of resistance at tºC.
\[\text{RTC at t}{}^\circ \text{C = }{{\alpha }_{t}}\]
\[=\frac{\text{Slope of the charecteristics}}{{{\text{R}}_{\text{t}}}}\]
\[\text{But slope = }\frac{{{R}_{t}}-{{R}_{0}}}{t-0}=\frac{{{R}_{t}}-{{R}_{0}}}{t}\]
And,
\[{{\alpha }_{0}}=\frac{\left( {{R}_{t}}-{{R}_{0}} \right)/t}{{{R}_{0}}}\]
\[{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{0}}}{{\text{R}}_{\text{0}}}\text{t = }{{\text{R}}_{\text{t}}}-{{\text{R}}_{\text{0}}}\]
\[{{\text{R}}_{\text{t}}}\text{= }{{\text{R}}_{\text{0}}}\text{( 1 + }{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{0}}}\text{t )}\]
We can generalize this expression by replacing t by t2 and 0 by t1 to get,
\[{{\text{R}}_{\text{t2}}}\text{= }{{\text{R}}_{\text{t1}}}\text{( 1 + }{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{t1}}}\Delta \text{t )}\]
Where,
Δt = Change in temperature = (t2 – t1)
αt1 = R.T.C. at t1ºC and Rt2 = Resistance at t2ºC.
Note :
Hence we conclude that the R.T.C. changes with the change in temperature. Higher the value of R.T.C. and R.T.C is maximum at 0ºC.