The ratio of the phasor sum of E.M.Fs induced in all the coils distributed in a number of slots under one pole to the arithmetic sum of the E.M.Fs induced is known as distribution factor (Kd). It is also known as breadth factor (Kb).
Distribution factor,
Kd =EMF induced in distributed winding / EMF induced if the winding would have been concentrated
\[=\frac{\text{Phasor sum of E}\text{.M}\text{.F components}}{\text{Arithmetic sum of E}\text{.M}\text{.F components}}\]
The distribution factor is always less than unity.
Derivation for Distribution Factor
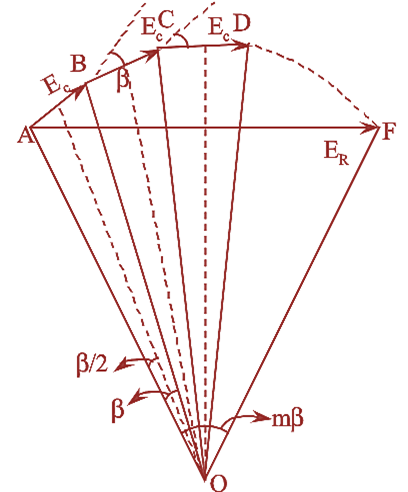
Figure 1.
Let,
Number of slots/pole/phase = m
Number of slots/pole = n
E.M.F induced in each coil side = Ec
Angular displacement between the slots = β
Where,
\[\beta =\frac{180{}^\circ }{n}\]
Phase spread angle = mβ in radians or electrical degrees.
The E.M.F induced in different coils of one phase under one pole are represented by AB, BC and CD. They are equal in magnitude and differ in phase by each other and are shown in figure (1).
E.M.Fs induced in each coil side are equal in magnitude = Ec = E.
\[E=AB\times 2\times OA\times \sin \frac{\beta }{2}\]
\[\text{Arithmetic sum = }m\times 2\times OA\times \sin \frac{\beta }{2}\]
ER = The resultant E.M.F induced in one polar group of one phase and is represented by the phasor AF in figure (1)
The resultant E.M.F will be,
\[{{E}_{R}}=OF\]
\[=2\times OA\times \sin \frac{AOF}{2}\]
\[=2\times OA\times \sin \frac{m\beta }{2}\]
Now, distribution factor (Kd) is given by,
Phasor sum of E.M.F components
\[{{K}_{d}}=\frac{\text{Phasor sum E}\text{.M}\text{.F components}}{\text{Arithmetic sum E}\text{.M}\text{.F components}}\]
\[{{K}_{d}}=\frac{2\times OA\times \sin \frac{m\beta }{2}}{2\times OA\times \sin \frac{AOF}{2}}\]
\[{{K}_{d}}=\frac{\sin \frac{m\beta }{2}}{m\sin \frac{\beta }{2}}\]
This equation is for fundamental component of E.M.F.
If flux distribution contains space harmonics, the slot angular pitch β would be ‘rβ’ for the rth harmonic component, then distribution factor for rth harmonic component,
\[{{K}_{dr}}=\frac{\sin r\frac{m\beta }{2}}{m\sin \frac{r\beta }{2}}\]
Distribution factor reduces the number of conductors per slot thereby, temperature rise at centre of slot also reduces.