What is DC to DC Boost Converter? Working Principle, Waveforms, Circuit Diagram, Formula & Derivation

A boost converter set up the output voltage is more (i.e., stepped up) than the DC input voltage. Hence, this converter is called boost converter.

Working Principle of Boost Converter

The line voltage on rectification gives unregulated D.C voltage, which fluctuates due to the changes in magnitude of the line voltage. This unregulated D.C voltage is given as input to the boost converter to obtain the required controlled DC output voltage. This required control is obtained by varying the duty cycle from 0 to 1 which varies the output voltage, E_o from E_d.c to ∞ which is a stepped up output voltage.

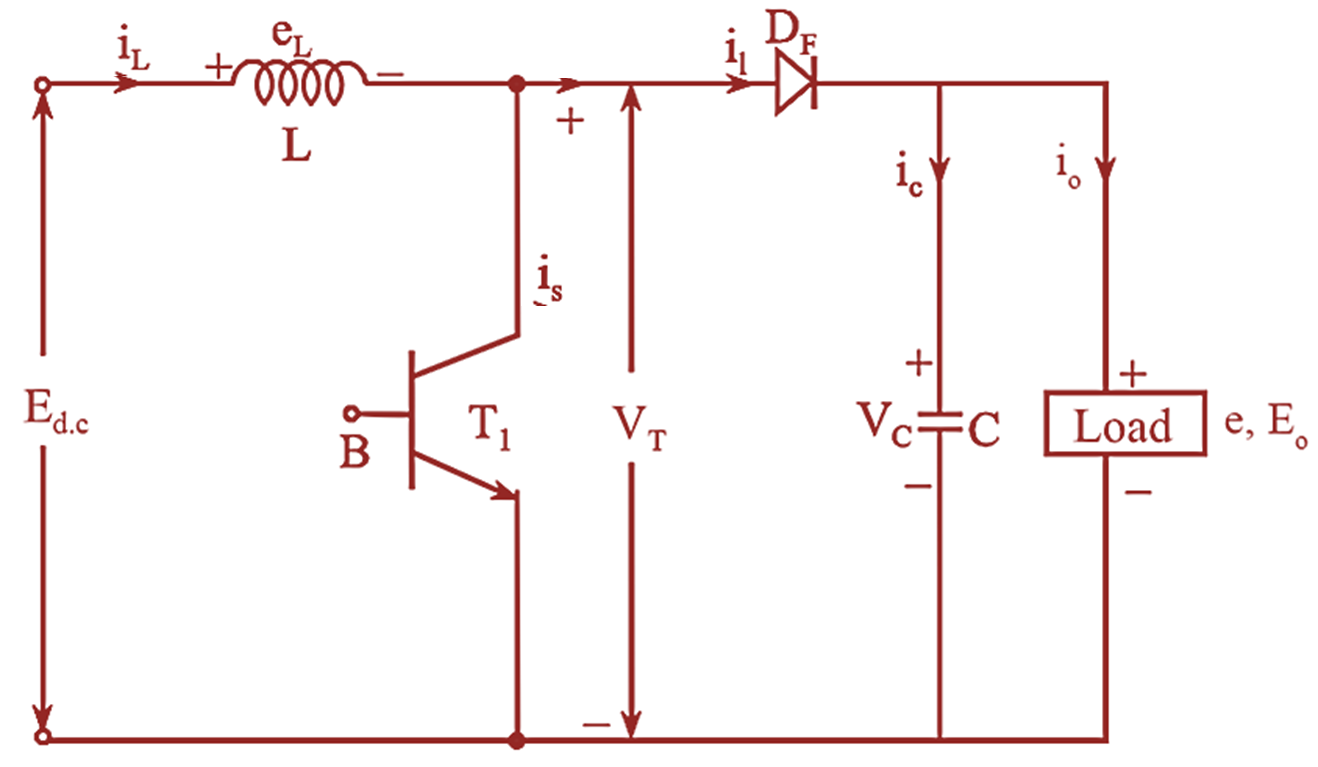
Figure 1: Circuit Diagram of Boost Converter.

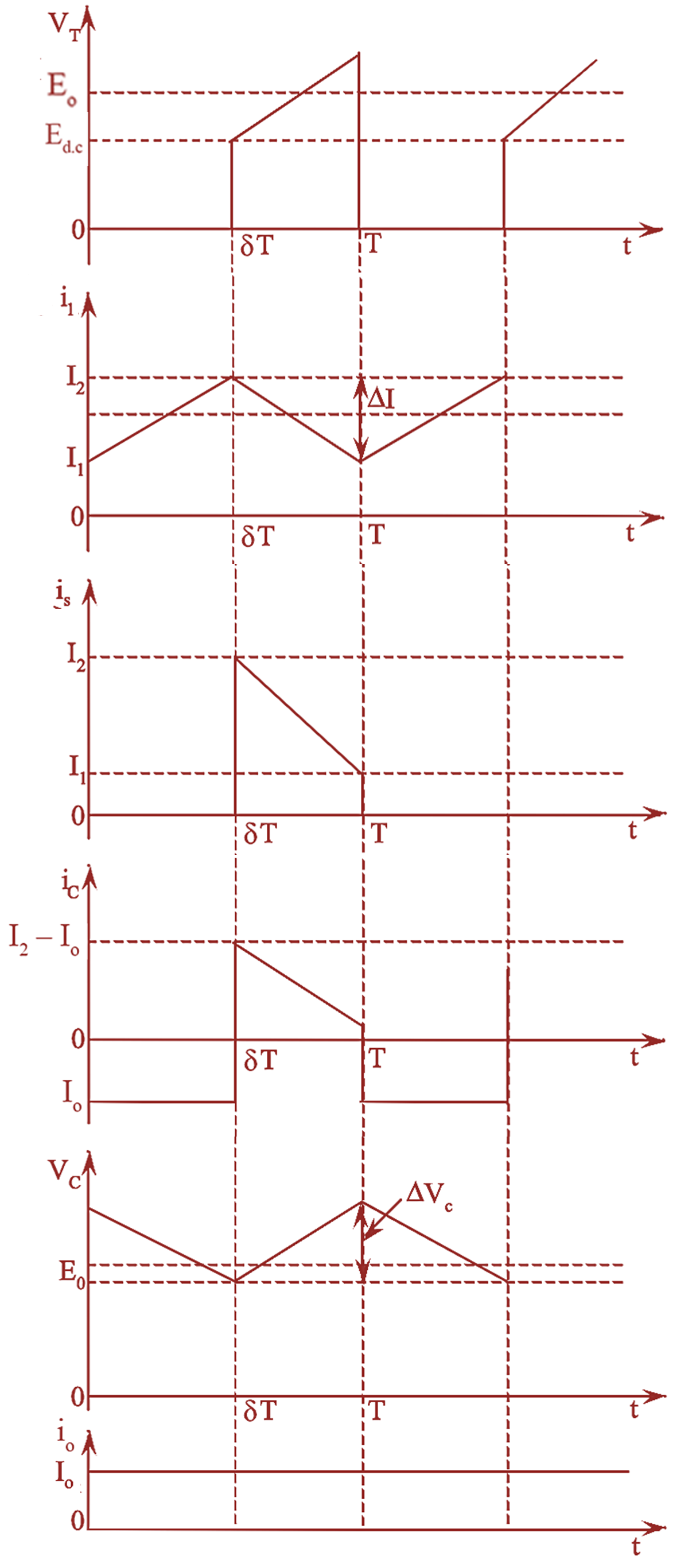
Figure 2: Waveforms of Boost Converter.

Figure (1) shows the circuit setup of boost converter and figure (2) depicts the voltage and current waveforms for a continuous inductor current. The operation of the boost converter can be explained in two modes.

Mode 1

At t = 0, power transistor is turned ON.

The rising input current flows through the inductor L and the transistor T_l. The inductor connected to the supply E_d.c, stores energy during this period. Thus from the circuit diagram of figure (1) it can be seen that the diode D_F would be reverse biased thus isolating the output stage. The equivalent circuit for mode 1 is as shown in figure (3).

Mode 2

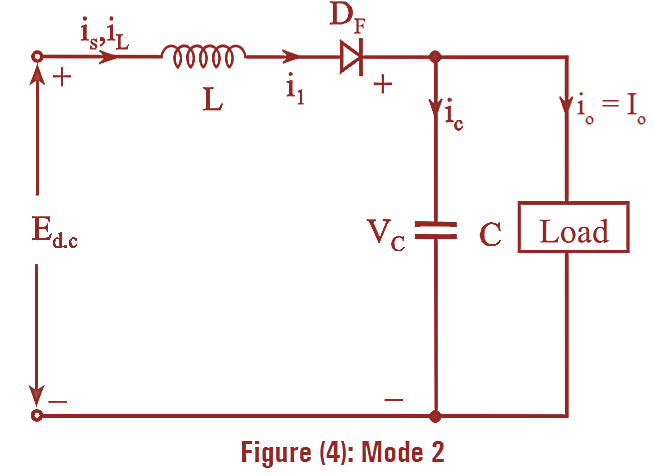
At t = T_ON, Transistor is switched OFF

During this period the current flows through L – D_f – C — load. The energy stored in the inductor, L is transferred to the output stage and the current in the inductor reduces till the transistor is turned ON in the next cycle. The equivalent circuit for the operation of mode 2 is as shown in figure (4).

Derivation for Boost Converter

Assuming a linear rise in the inductor current from I₁ to I₂, we get,

\[{{E}_{d.c}}=L\left( \frac{{{I}_{2}}-{{I}_{1}}}{{{T}_{ON}}} \right)\]

\[{{E}_{d.c}}=L\frac{\Delta I}{{{T}_{ON}}}…(1)\]

\[{{T}_{ON}}=L\frac{\Delta I}{{{E}_{d.c}}}…(2)\]

Also, assuming a linear fall in the inductor current at t = T_OFF from I₂ to I₁, we get

\[{{E}_{d.c}}-{{E}_{o}}=-L\frac{{{I}_{2}}-{{I}_{1}}}{{{T}_{OFF}}}\]

\[{{E}_{d.c}}-{{E}_{o}}=-L\frac{\Delta I}{{{T}_{OFF}}}…(3)\]

\[{{T}_{OFF}}=L\frac{\Delta I}{\left( {{E}_{o}}-{{E}_{d.c}} \right)}…(4)\]

Where, ΔI = (I₂ – I₁) is the peak-to-peak ripple current of the inductor L.

Now, from equation (2) and equation (4) the peak-to- peak ripple current of the inductor L is obtained as,

\[\Delta I={{E}_{d.c}}\frac{{{T}_{ON}}}{L}=\left( {{E}_{o}}-{{E}_{d.c}} \right)\frac{{{T}_{OFF}}}{L}…(5)\]

Substituting T_ON = δT and T_OFF = (l – δ) T, we get,

Average output voltage,

\[{{E}_{o}}={{E}_{d.c}}\frac{T}{{{T}_{off}}}=\frac{{{E}_{d.c}}T}{\left( 1-\delta  \right)}\]

\[=\frac{{{E}_{d.c}}}{\left( 1-\delta  \right)}\]

By interchanging equation (6), we get,

Voltage gain,

\[\frac{{{E}_{o}}}{{{E}_{d.c}}}=\frac{1}{\left( 1-\delta  \right)}\]

Advantages of Boost Converter

1. A boost converter can step-up the output voltage without a transformer
2. The circuitry of boost converter requires only one transistor (switch) and hence its efficiency is high.

Disadvantages of Boost Converter

1. High peak current flows through the power transistor.
2. Stabilizing the regulator may be difficult as the output voltage is very sensitive to changes in duty cycle.
3. Require large filter capacitor and large inductors.

Applications of Boost Converter

1. A boost converter finds its application in regulated D.C power supplies.
2. It is used in the regenerative braking of D.C motors.