Torque Production in DC Motor
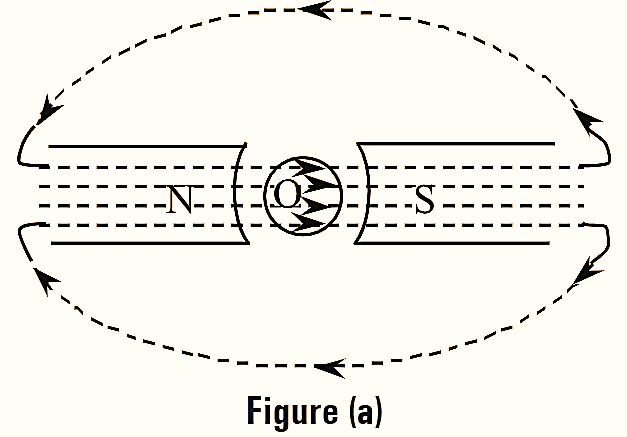
Consider a DC motor with stator and rotor. When the stator coils are energized, a stator magnetic flux is set up and follows the path as shown in figure (a) with no current in the rotor conductor.
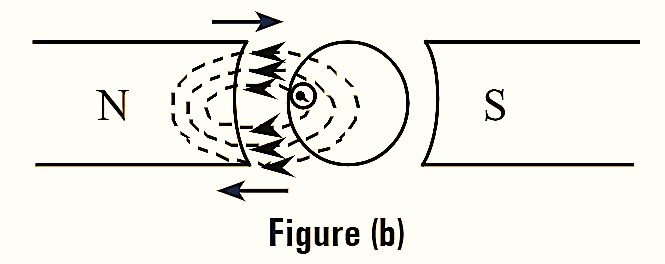
When rotor conductor carries current. magnetic flux is set up and flows in the direction as shown in figure (b) with no current in the stator coil.
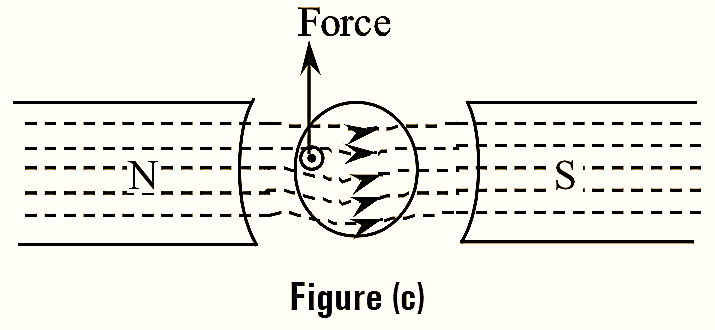
Now when both the stator coil and the rotor conductor carries current, then an interaction between the stator flux and the flux produced by the rotor takes place and the resultant magnetic field is set up as shown in figure (c). The rotor conductors experience a force in the upward direction and develop a torque. Thus, the torque is produced in a DC motor when the stator flux and flux produced by the rotor conductor interacts with each other.
Derivation for Torque Equation of a DC Motor

Let,
F — Force in Newton
r — Radius of armature in meter
Ta — Armature torque in N-m
S — Circumferential distance
f — Flux/pole in Wb
P — Number of poles
Z — Number of armature conductors
A — Number of armature paths
Ia — Armature current
N — Speed of armature in r.p.m. Since, torque is the twisting movement produced across the armature.
\(\frac{N}{60}\) = Speed in r.p.m
dt = \(\frac{60}{N}\) = Time taken for one revolution.
Mechanical work done per second is given as,
\[\text{Mechanical W}\text{.D / sec = }\frac{F\times \text{ Circumferential distance}}{\text{Time}}\]
\[=\frac{F\times S}{{}^{60}/{}_{N}}\]
\[=F\times 2\pi r\times \frac{N}{60}\text{ }\left[ S=2\pi r \right]\]
\[=F\times r\times \frac{2\pi N}{60}\]
\[=\frac{{{T}_{a}}\times 2\pi N}{60}\text{ N-m / sec }\left[ {{T}_{a}}=F\times r \right]\]
The electrical work done per second,
\[\text{Electrical W}\text{.D / sec = }{{E}_{b}}\times {{I}_{a}}\]
\[=\frac{\phi PN}{60}\times \frac{Z}{A}{{I}_{a}}\text{ }\left[ {{E}_{b}}=\frac{\phi PN}{60}\times \frac{Z}{A} \right]\]
As 1 N-m/sec= 1 watt, equating mechanical and electrical power, we get,
\[\frac{{{T}_{a}}\times 2\pi N}{60}=\frac{\phi PN}{60}\times \frac{Z}{A}{{I}_{a}}\]
\[{{T}_{a}}\times 2\pi =\frac{\phi PZ{{I}_{a}}}{A}\]
\[{{T}_{a}}=\frac{1}{2\pi }\times \frac{\phi PZ{{I}_{a}}}{A}\]
\[{{T}_{a}}=\frac{0.159}{9.81}\frac{\phi PZ{{I}_{a}}}{A}\text{ kg-m}\]
\[{{T}_{a}}=\frac{0.0162\phi PZ{{I}_{a}}}{A}\text{ kg-m (MKS}\text{ unit)}\]
Shaft Torque
Shaft torque is the torque which is available for doing useful work. It is usually denoted by T and is always available at the shaft.
\[\text{Motor output = }\omega {{\text{T}}_{sh}}\text{ watts = }\frac{2\pi N}{60}.{{T}_{sh}}\text{ watts}\]
Shaft torque,
\[{{\text{T}}_{sh}}=\frac{\text{Output in watts}}{\frac{2\pi N}{60}}\]
\[=\frac{60}{2\pi }\times \frac{\text{Output}}{N}\text{ N-m = 9}\text{.55 }\times \text{ }\frac{\text{Output}}{N}\text{ N-m}\]
Lost Torque
When the mechanical power developed is transmitted to the shaft of the motor, there occurs a power loss due to friction, windage and iron loss. Therefore the torque required to overcome these losses is known as lost torque or lost torque. The total armature torque is the combination of shaft torque and lost torque.
\[{{T}_{a}}={{T}_{sh}}+{{T}_{f}}\]
Lost torque,
\[{{T}_{f}}={{T}_{a}}-{{T}_{sh}}\]