Swinburne’s test is the simplest indirect method to determine the efficiency of D.C machine. In this test the no- load losses are measured separately and from their knowledge, efficiency at any desired load can be predetermined in advance.
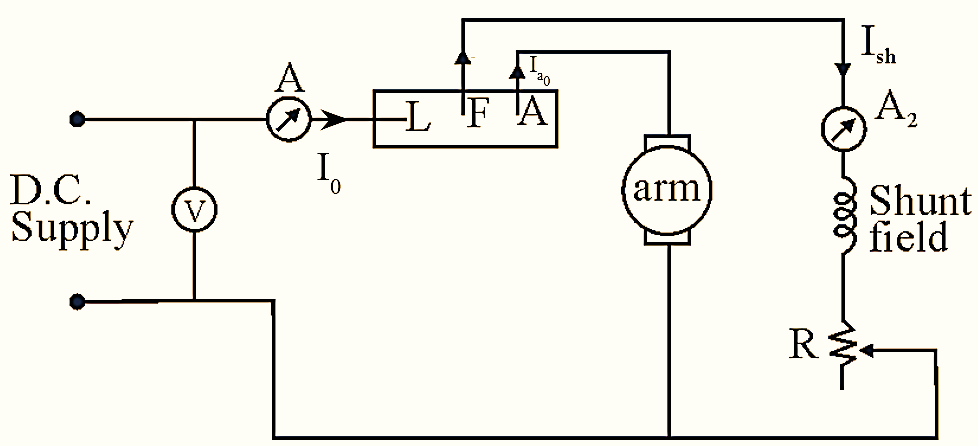
Figure 1: Arrangement of Swinburne’s test.
In Swinburne’s test, R and are measured separately so that losses can be calculated easily on various loads. The machine whether motor or generator is run as a shunt motor on no-load, the field rheostat is adjusted to give rated speed and rated voltage when shunt is applied across the terminals of motor.
The circuit diagram for determining the no-load losses of a D.C shunt machine is shown in figure.
Let,
V is the voltage measured by voltmeter
I0 is the input motor current which is measured by ammeter A1.
Ish is the shunt field current measured by ammeter A2.
We know that,
Input power Output + Losses
Since machine is on no-load,
Input power = Losses [Since, Output = 0]
From the above equation, it is clear that no-load input power is used to supply internal losses in the machine that is shunt field copper loss, armature copper loss, stray losses in shunt machine.
Power input = VI0
Shunt field copper loss = VIsh
Armature copper loss = I2a0 = (I0 – Ish)2Ra
Here, Ra is the Armature resistance. Since,
Power input = Total losses
\[V{{I}_{0}}=V{{I}_{sh}}+I_{{{a}_{0}}}^{2}{{R}_{a}}+\text{ Strey losses}\]
\[\text{Strey losses}=V{{I}_{0}}-V{{I}_{sh}}-{{({{I}_{0}}-{{I}_{sh}})}^{2}}{{R}_{a}}\]
If the shunt field copper loss is added to stray loss then the constant loss can be obtained which remains constant irrespective of the load on the machine.
Constant losses = Stray losses + Shunt copper losses
\[=V{{I}_{0}}-{{({{I}_{0}}-{{I}_{sh}})}^{2}}{{R}_{a}}\]
Since constant losses are known, the efficiency can be determined at any load. Let ‘I’ be the load current where the efficiency of machine is to be determined.
Efficiency when Running as Generator
Generator output = VI watts
Total losses = Armature copper loss + Field copper loss + Stray losses
\[=I_{a}^{2}{{R}_{a}}+{{W}_{c}}\]
\[={{(I+{{I}_{sh}})}^{2}}{{R}_{a}}+{{W}_{c}}\]
Input = Output + Losses
\[=VI+{{(I+{{I}_{sh}})}^{2}}{{R}_{a}}+{{W}_{c}}\]
\[\text{Efficiency = }\frac{\text{Output}}{\text{Input}}=\frac{VI}{VI+{{(I+{{I}_{sh}})}^{2}}+{{W}_{C}}}\]
Efficiency when Running as a Motor
Motor input = VI
Total losses = Armature copper loss + Wc
\[=I_{a}^{2}{{R}_{a}}+{{W}_{c}}\]
\[={{(I-{{I}_{sh}})}^{2}}{{R}_{a}}+{{W}_{c}}\]
Motor output = Input – Losses
\[=VI-{{(I-{{I}_{sh}})}^{2}}{{R}_{a}}-{{W}_{c}}\]
\[\text{Efficiency of motor = }\frac{\text{Output}}{\text{Input}}\]
\[=\frac{VI-{{(I-{{I}_{sh}})}^{2}}{{R}_{a}}-{{W}_{c}}}{VI}\]