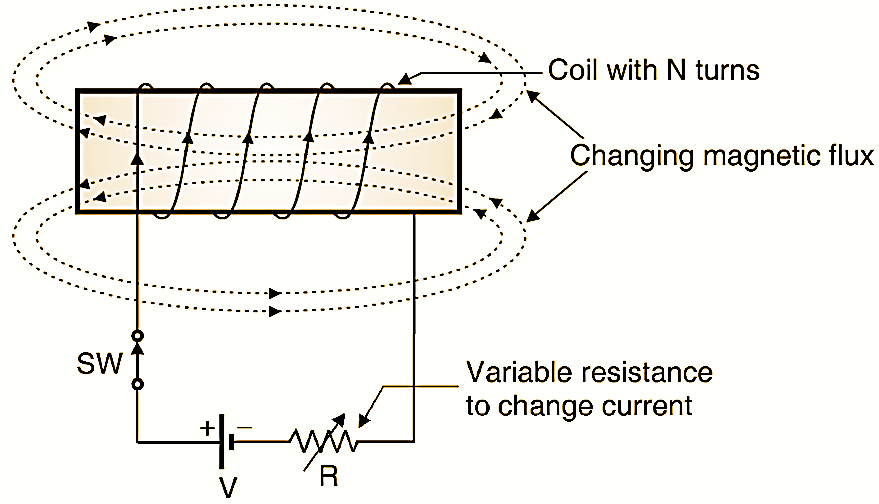
Figure 1: Setup to understand the concept of self inductance.
Definition of Self inductance
As per the Lenz’s law, the self-induced emf opposes any current change taking place. This property of the coil to oppose any change in current flowing through it is known as the self-inductance or inductance. As per the Faraday’s law of electromagnetic induction, the magnitude of the self induced emf in a coil (refer Fig. 1) due to change in current flowing through it is given by,
\[e=-N\frac{d\phi }{dt}\]
where the negative sign indicates that the self induced voltage opposes the change in current through the coil.
Meaning of Self inductance
If the current through the coil (I) produces a flux (ϕ) Webers then the self inductance is given by,
\[\text{Inductance (L) = }\frac{N\times \phi }{I}….(1)\]
Thus, self inductance (L) is defined as the ratio of the flux linkage Wb meter (N × ϕ) to the current I. The units of inductance is Wb Turn / Ampere or Henry. Substituting \(\phi =\frac{L\times I}{N}\) into equation (1) we get,
\[e=-L\left[ \frac{dI}{dt} \right]\text{ Volts}\]
Formula for Self Inductance
We have defined the co-efficient of inductance (L) as,
\[\text{L=}\frac{N\times \phi }{I}\text{ Henry}\]
\[\phi =\frac{m.m.f}{{Re}luc\tan ce}=\frac{N\times I}{S}\]
\[ L=\frac{N}{I}\left[ \frac{N\times I}{S} \right]=\frac{{{N}^{2}}}{S}\text{ Henry}\]
But reluctance,
\[S=\frac{l}{{{\mu }_{0}}{{\mu }_{r}}a}\]
\[L=\frac{{{N}^{2}}\times {{\mu }_{0}}{{\mu }_{r}}a}{l}\text{ Henry}…(1)\]
Where
l = Length of the magnetic circuit ,
µr = Relative permeability ,
a = Cross sectional area of magnetic circuit.
N = Number of turns.
Factors Affecting the Self Inductance (L)
From Equation (1) the factors influencing the self inductance are :
- The self-inductance L is proportional to the square of the number of turns of the coil i.e. N2.
- L is directly proportional to the cross sectional area “a” of the magnetic circuit.
- L is inversely proportional to the length (l) of the magnetic circuit.
- L is directly proportional to the relative Permeability µr of the material of the magnetic circuit (core).
- The value of relative permeability µr is dependent on the magnetic flux density (B) because µ = B/H. Hence, the self-inductance (L) also is dependent on the value of flux density B.