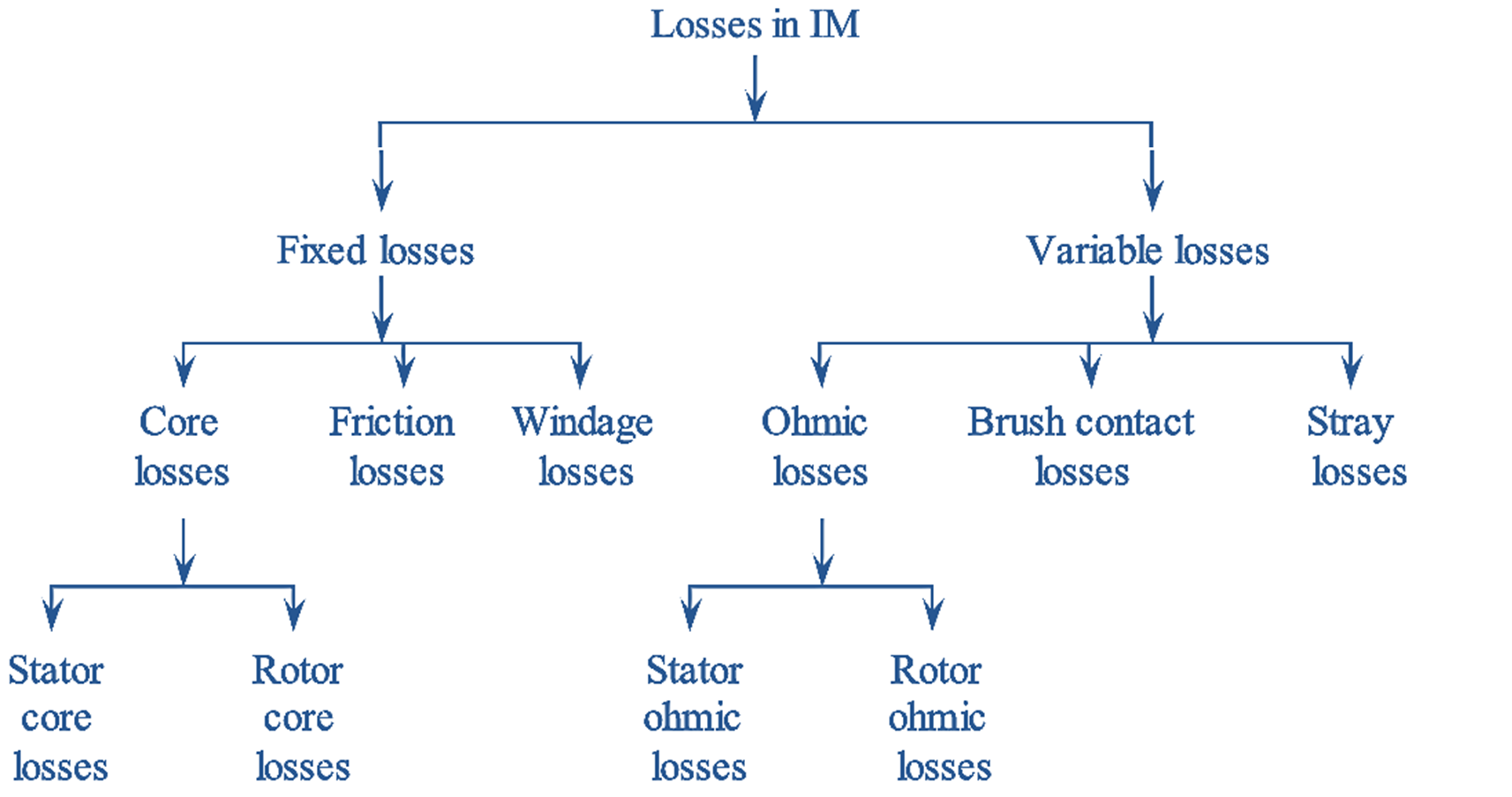
Figure 1: Losses in Induction Motor.
Losses in an Induction Motor
The various losses taking place in induction motor are categorized as shown in the following figure 1. The losses which occur whenever the motor is energized and remain constant for any given voltage and speed are known as fixed losses. Core losses, friction losses and windage losses are fixed losses. These losses are known as fixed losses because the speed of the induction motor changes very slightly when compared with the actual speed and the frequency is also very small.
Therefore the core losses due to stator, rotor and the friction losses also remain constant. All the core losses, friction losses and windage losses remain constant and these losses together are termed as constant rotational losses. The no-load test of the induction motor gives the fixed losses of the motor. The losses which increase with an increase in motor load are called variable losses. Variable losses include stator ohmic losses, rotor ohmic losses, stray losses and brush contact losses. The ohmic losses occur due to the resistance in stator and rotor windings. As a result heat is generated whenever a current is passed, which is proportional to resistance of the material and square of the current. The stray losses arise due to variety of sources proportional to square of the rotor current. Since, these losses vary as a function of motor loading, they are known as variable losses. The stator and rotor ohmic losses can be known from ‘blocked rotor test’.
Efficiency of Induction Motor
Efficiency of the motor is the ratio of mechanical energy output divided by the electrical energy input i.e.,
\[\eta =\frac{{{P}_{out}}}{{{P}_{in}}}\] Let,
Pshaft = Power at the shaft of the rotor
PStator core = Stator core losses
PStator I2R = Stator I2R losses
PRotor core = Rotor core losses
P Rotor I2R = Rotor I2R losses
PF&W = Friction and windage losses
Pc = Constant or fixed losses
PI2R = Ohmic losses
Padditional = Stray load losses and brush contact losses.
Then,
\[{{P}_{c}}={{P}_{\text{Stator core }}}+{{P}_{\text{Rotor core }}}+{{P}_{\text{F }\!\!\And\!\!\text{ W}}}\]
\[{{P}_{{{\text{I}}^{\text{2}}}\text{R}}}={{P}_{\text{Stator }{{\text{I}}^{\text{2}}}\text{R }}}+{{P}_{\text{Rotor }{{\text{I}}^{\text{2}}}\text{R }}}+{{P}_{\text{additional}}}\]
By taking into account all these losses, the efficiency of induction motor is calculated as,
\[\eta =\frac{{{P}_{\text{shaft}}}}{{{P}_{\text{shaft}}}+{{P}_{c}}+{{P}_{{{I}^{2}}r}}}\times 100\]