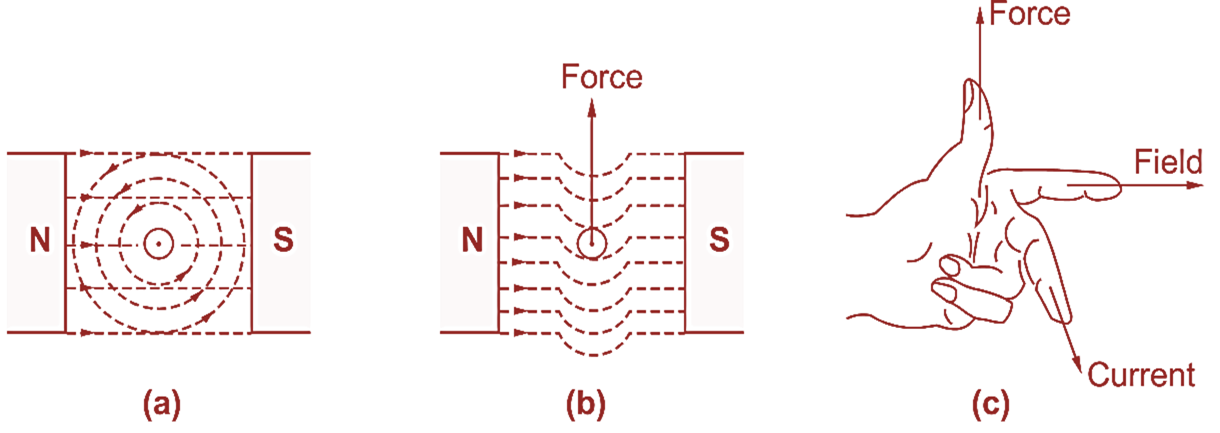
Figure 1. Force acting on a Current Carrying Conductor placed in a Magnetic Field.
It is observed that whenever a current carrying straight conductor is placed in a magnetic field, it experiences a mechanical force. This is a very important magnetic effect of an electric current as the operation of the electric motors and other electrical appliances is entirely based on this effect. The magnitude of this force is dependent on the following factors:
- Flux density (B) of the magnetic field in which the conductor is placed (in tesla).
- Magnitude of the current (I) in the conductor (in amperes).
- Active length (l) of the conductor (in metres). Active length is the part of the total length of the conductor which actually lies in the magnetic field.
If the conductor is at right angles to the magnetic field, then this force (F) is given by the following expression :
\[\text{F=B I }l\text{ newton}….(1)\]
It will be interesting to see how this force is actually produced. Fig. 1 (a) shows a straight conductor carrying current in the direction towards the observer and placed in a uniform magnetic field at right angles to it. The original field and that due to the conductor are also shown in Fig. 1 (a). These two fields combine to form a single resultant field. It will be seen that in the region below the conductor, both the fields act in the same direction and therefore give a resultant field at any point equal to the sum of the individual fields at that point. In the region above the conductor, one field acts in the direction opposite to that of other and so the resultant is the difference of the two fields. In general, the original field of the magnet is strengthened at the bottom of conductor and weakened at the top. The resultant field pattern is shown in Fig. 1 (b) effect, it seems as if some of the lines of force from the top region are transferred to bottom region.
Due to crowding, the lines of force in the lower region get stretched like rubber bands. Therefore, they try to contract and thereby push the conductor upwards. Thus, conductor experiences a mechanical force in the upward direction. If the direction of the current in the conductor or the direction of the main field reversed, the direction of force exerted on the conductor is also reversed. The direct of the force can be easily found by Fleming’s left hand rule.
Fleming’s Left Hand Rule :
Arrange the first finger, the second finger and the thumb of your left hand mutually at right angles to one another (Fig. 1 c). Point the first finger in the direction of the field and the second finger in the direction of the current, then the thumb will point in the direction of the force on the conductor.
On applying the above rule to the conductor which we have considered, it will be readily found that it experiences a mechanical force in the upward direction. In general, if the current carrying conductor under consideration in the above case is assumed to be making an angle θ with the direction of the field, then the Expression (1) for the force experienced by it will obviously get modified as follows :
\[\text{F = B I }l\text{ sin}\theta \text{ newton}\]
Where,
l sinθ = Component of the active length of the conductor at right- angles to the flux.