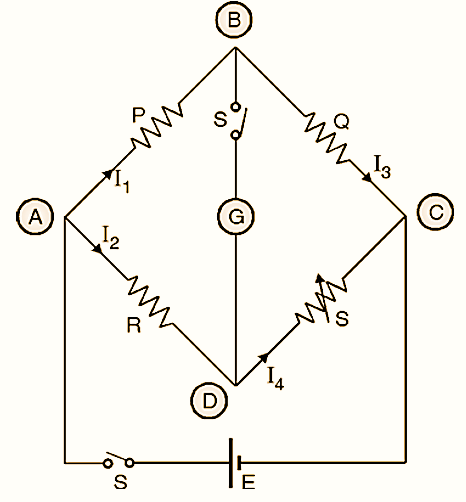
Figure 1: Wheatstone Bridge.
Wheatstone bridge has its own importance and it is used from the very old days and proves to be important and reliable even today for measurement of unknown resistance by comparison method.
Construction of Wheatstone Bridge
In its simplest form, it has 4-arms connected in diamond shape. 3-arms have the resistances P, Q and S and R arm for connecting unknown resistance whose value is to be determined. S-resistance is adjustable variable resistance and P and Q are the ratio arms of multiple value resistances 10, 100, 1000,………
These 4-arms are connected at the junctions ABC and source voltage (Battery of 1.5 Volts) is connected across A and C. Galvanometer is connected across terminals B and D.
Steps in Wheatstone Bridge Balancing and Balancing Equation
Battery and galvanometer are connected as shown in the circuits unknown resistance R is connected across X1 X2 key (or switch S) is pressed to commence (see Figure 1). The values of P and Q ratio are selected. Resistance ‘S’ is varied. Initially the currents in branch are different as I1, I2, I3 and I4 and also galvanometer deflects in either direction. P, Q and ‘S’ are so adjusted that galvanometer shows zero (Null-point) reading. This condition is known as balanced condition or null condition of bridge. In balanced condition, current in the upper two branches through P and Q is same and in the lower branches through R and S is same. When there is no current in the galvanometer the points B and D are equipotential points.
Potential difference across AB = Potential difference across AD
\[{{I}_{1}}P={{I}_{2}}R….(1)\]
Also, Potential difference across BC = Potential difference across CD
\[{{I}_{3}}Q={{I}_{4}}S….(2)\]
Current in the upper branch will be same throughout say Il and current in the lower branch will be same throughout say I2.
\[{{I}_{3}}={{I}_{1}}\]
\[\text{And }{{I}_{4}}={{I}_{2}}\]
\[{{I}_{1}}P={{I}_{2}}P….(3)\]
\[\text{And }{{I}_{1}}Q={{I}_{2}}S….(4)\]
Dividing equation (1) by equation (3),
\[\frac{{{I}_{1}}P}{{{I}_{1}}Q}=\frac{{{I}_{2}}R}{{{I}_{2}}S}\]
\[\frac{P}{Q}=\frac{R}{S}\]
\[\text{Unknown resistance }R=S\times \frac{P}{Q}\]
This is the equation of Wheat stone bridge at balance. Thus unknown resistance R is found from ratio arm resistance P and Q and variable resistance S.
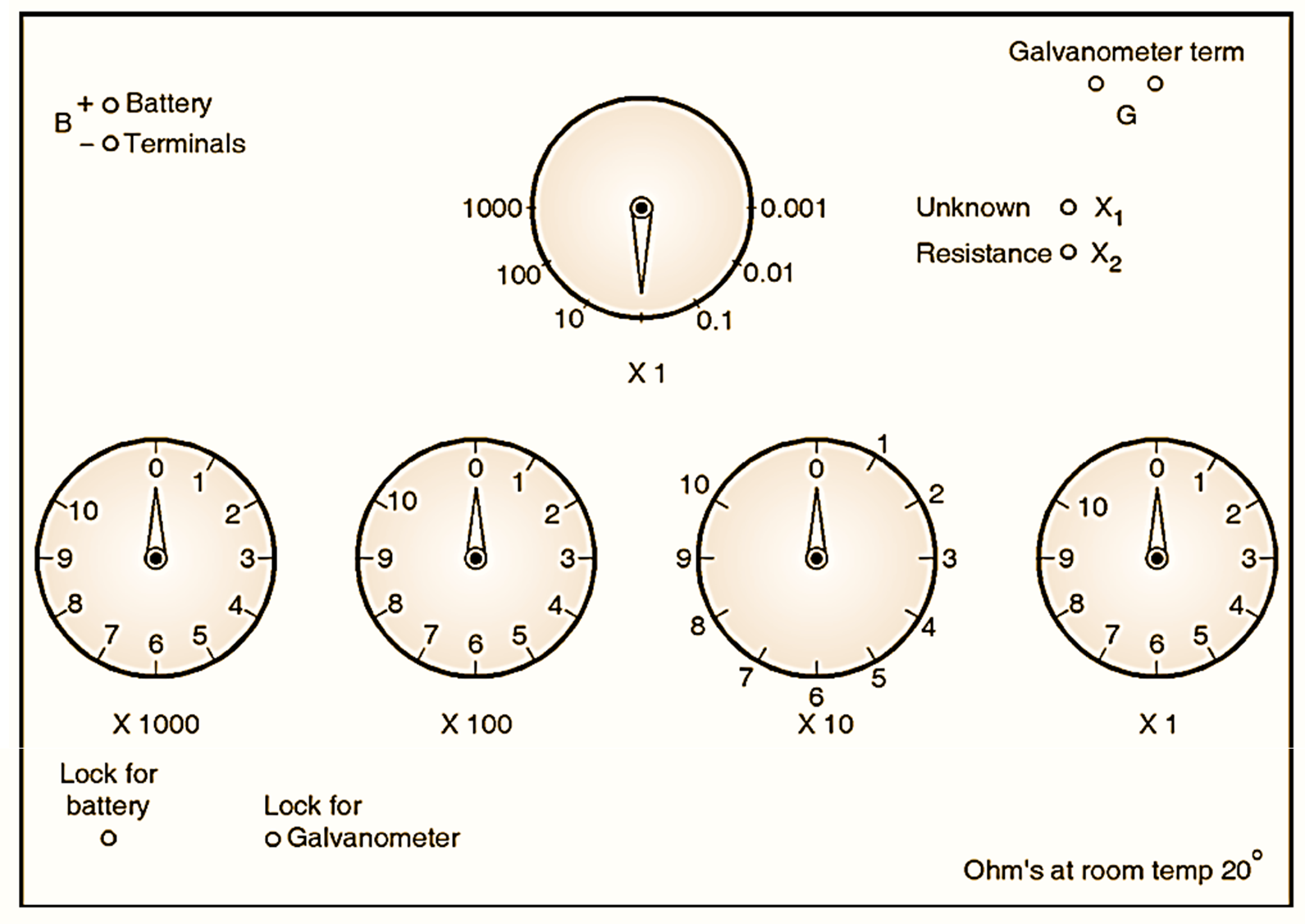
Figure 2: Control panel of Wheatstone Bridge.
Resistances P, Q and S are mounted inside Wheatstone bridge box with adjusting knobs on the box-plate (see Figure 2) for operation. P and Q normally consistence of 4-resistors each, the values being 10, 100, 1000, 10000. Resistor ‘S’ consists of a 4-dial or 5 dial decade arrangement of resistors.
Errors Present in Wheatstone Bridge or Limitations / Disadvantages of Wheatstone Bridge :
Following errors are present in Wheatstone bridge :
Errors Present in Wheatstone Bridge,
- Contact resistance
- Thermoelectric
- Effect of temperature
- Other errors
1. Contact resistance
This can cause serious error when comparatively low resistance is measured. If the contact resistance of connecting leads, terminals is greater than the unknown resistance, a serious error is introduced.
2. Thermoelectric emf
Thermo electric emfs are present in the measuring circuit which cause error.
3. Effect of temperature
The standard resistances used in the bridge circuit may suffer from temperature variations. This happens because of self heating effect (IR). E.g. If resistances in the bridge are wire wound resistances and made up of copper, with temperature coefficient of 0.004/ºC. Thus if temperature changes by 1ºC the error caused is 0.4%.
4. Other errors
The bridge should be precisely balanced so if human error is involved, there will be error in measurement. The galvanometer used should be sensitive otherwise null condition cannot be detected accurately.