What is UJT Relaxation Oscillator? Working, Circuit Diagram, Waveforms & Derivation

UJT Relaxation Oscillator is a nonlinear oscillator which generates a non-sinusoidal signal such as sawtooth waveforms as output.

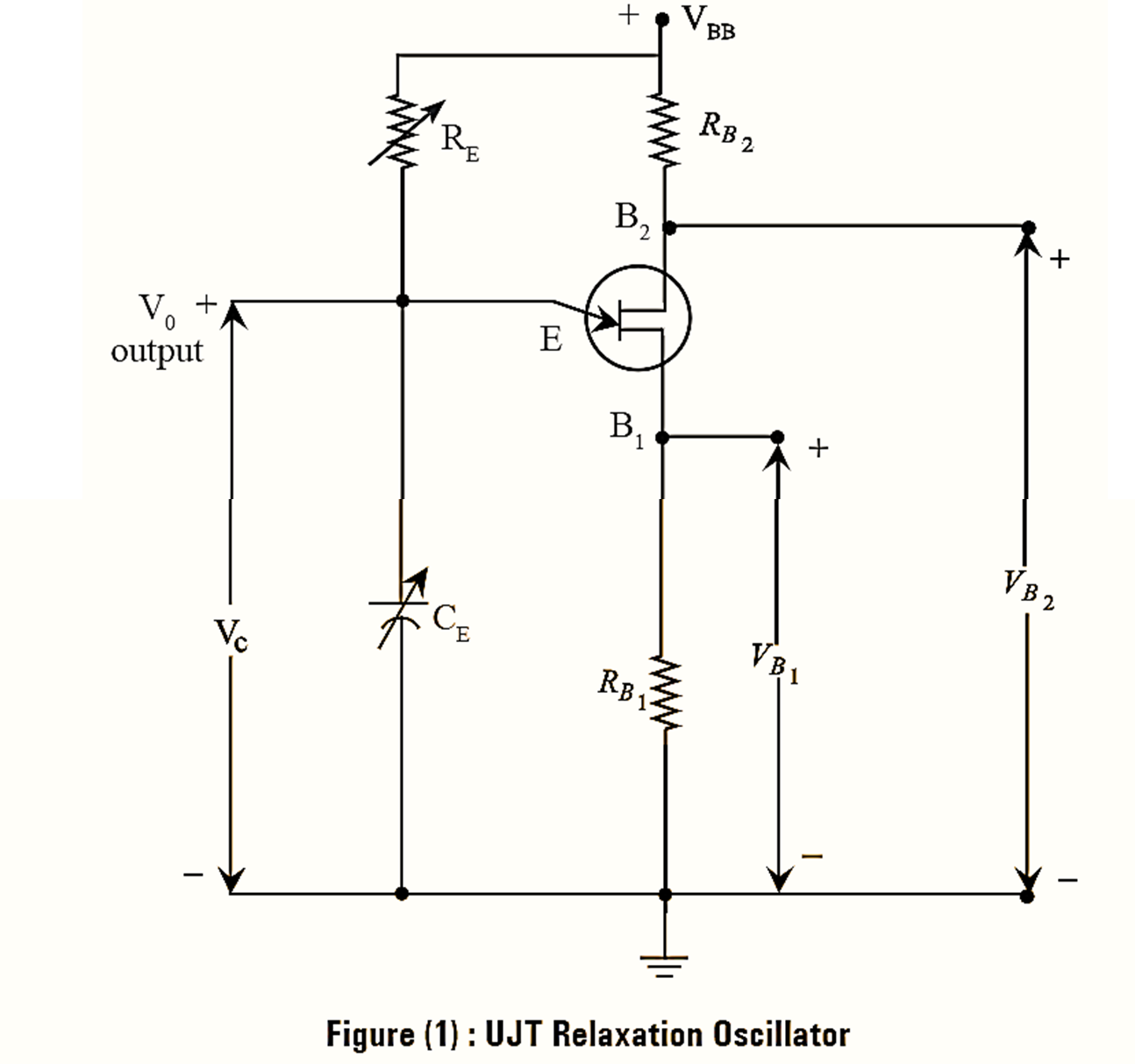
Circuit Diagram for UJT Relaxation Oscillator

The circuit diagram for UJT Relaxation Oscillator is as illustrated in figure (1). The circuit includes a variable resistor R_E and capacitor C_E across the emitter terminal. The capacitor, C_E charges through the emitter resistor R_E when the supply V_BB is ON. The capacitor charges to peak value i.e., peak-point voltage V_P and turns UJT ON.

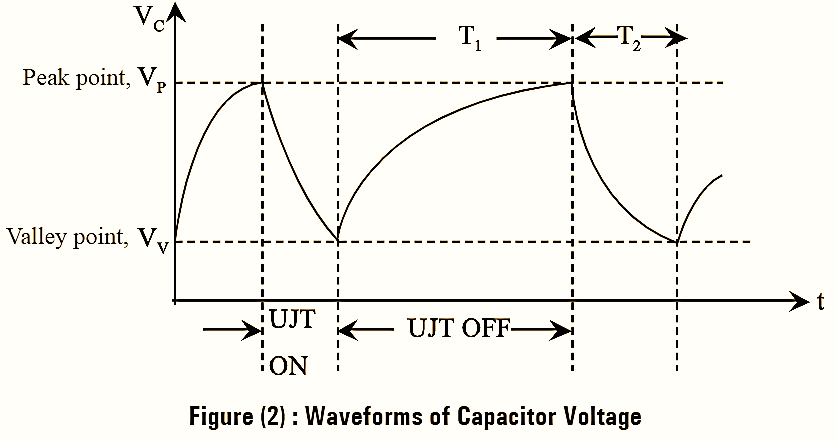
Then, the capacitor discharges through the resistor R_B1 and provides negative resistance, due to this UJT acts as relaxation oscillator. UJT conducts till, the voltage across the capacitor reaches to valley point V_V and again the process of capacitor charging and discharging repeats. Thus, it provides a sawtooth wave form at its output as shown in figure (2). The base resistance R_B1 and R_B2 generates spike wave forms. When UJT conducts, the current flows through R_B1 results a small potential drop across it, that provides a positive going spike. Similarly, the increase in current across resistor R_B2 gives a negative going spike. The variable capacitor, C and resistor, R can be timed to a desired value to attain certain frequency. Since, the time constant depends on these values and is expressed as,

τ = RC

Frequency of Oscillation

The drop across the capacitor, C is given by,

\[{{V}_{C}}={{V}_{BB}}(1-{{e}^{-t}}^{/RC})\]

The time taken for charging capacitor to a peak point voltage is obtained as follows.

\[{{V}_{C}}(\text{ charging })={{V}_{V}}+({{V}_{BB}}-{{V}_{V}})(1-{{e}^{-t}}^{/RC})\]

\[={{V}_{V}}+{{V}_{BB}}(1-{{e}^{-t}}^{/RC})-{{V}_{V}}+{{V}_{V}}{{e}^{-t}}^{/RC}\]

\[={{V}_{BB}}-({{V}_{BB}}-{{V}_{V}}){{e}^{-t}}^{/RC}\]

Since, V_C = V_P at t = T₁,

\[{{V}_{P}}={{V}_{BB}}-({{V}_{BB}}-{{V}_{V}}){{e}^{-{{T}_{1}}}}^{/RC}\]

\[{{V}_{BB}}-{{V}_{P}}=({{V}_{BB}}-{{V}_{V}}){{e}^{-{{T}_{1}}}}^{/RC}\]

\[-\frac{{{T}_{1}}}{{{R}_{C}}}=\text{ ln}\left( \frac{{{V}_{BB}}-{{V}_{P}}}{{{V}_{BB}}-{{V}_{V}}} \right)\]

\[{{T}_{1}}=RC\text{ ln }\left( \frac{{{V}_{BB}}-{{V}_{V}}}{{{V}_{BB}}-{{V}_{P}}} \right)….(1)\]

Similarly, the discharging period T₂ given by,

\[{{V}_{C}}={{V}_{P}}{{e}^{-t/RC}}\]

\[\frac{{{V}_{C}}}{{{V}_{P}}}={{e}^{-{{T}_{2}}/RC}}\]

Since, at t = T₂, V_C = V_V, we get.

\[\frac{{{V}_{V}}}{{{V}_{P}}}={{e}^{-{{T}_{2}}/RC}}\]

\[{{T}_{2}}=RC\text{ ln }\left( \frac{{{V}_{P}}}{{{V}_{V}}} \right)….(2)\]

The total time taken for charging and discharging of capacitor is evaluated as,

\[T={{T}_{1}}+{{T}_{2}}\simeq {{T}_{1}}\text{      }\left[ \text{ Since, } {{T}_{1}}>>{{T}_{2}} \right]\]

From equation (l), we get,

\[T=RC\text{ ln }\left( \frac{{{V}_{BB}}-{{V}_{V}}}{{{V}_{BB}}-{{V}_{P}}} \right)\]

Since, V_BB >> V_V above equation can be written as,

\[T=RC\text{ ln }\left( \frac{{{V}_{BB}}}{{{V}_{BB}}-{{V}_{P}}} \right)\]

\[=RC\text{ ln }\left( \frac{1}{1-\frac{{{V}_{P}}}{{{V}_{BB}}}} \right)\]

Since, V_P = ηV_BB + V_B and V_B is forward voltage of diode with a negligible value, T can be obtained as,

\[T=RC\text{ ln }\left( \frac{1}{1-\eta } \right)\]

\[=2.303\text{ lo}{{\text{g}}_{10}}\left( \frac{1}{1-\eta } \right)\]

The oscillating frequency of sawtooth wave is given by, \[{{f}_{o}}=\frac{1}{T}\]

\[{{f}_{o}}=\frac{1}{2.303\text{ RClo}{{\text{g}}_{10}}\left( \frac{1}{1-\eta } \right)}\]