According to the voltage division rule, the voltage across each resistor in a series electrical circuit is given by the ratio of product of the total voltage and that resistance to that of the sum of the resistances among which the voltage is divided.
Circuit Diagram & Derivation for Voltage Divider Rule
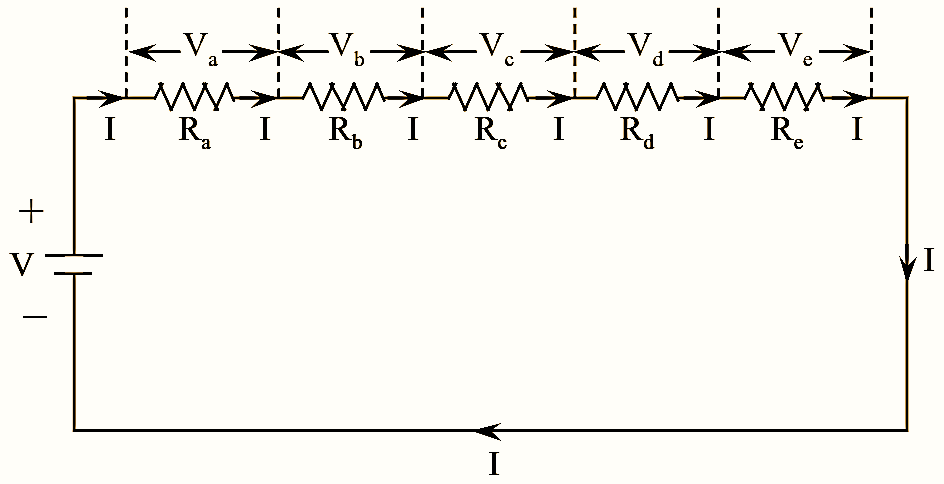
Figure 1: Series Circuit.
In order to understand the concept of voltage division rule. Consider a series electrical circuit as shown in figure 1. In this circuit, the current ‘I ‘ remains constant and is flowing through each resistor whereas voltage ‘ V ‘ is dropping at each resistor.
Hence, a series circuit acts as a voltage divider. The respective voltage drop in each resistor is proportional to the value of that resistor.
Voltage division rule is used to determine the various voltages across the circuit from a single source. From Ohm’s law, we know that,
Current,
\[I=\frac{V}{R}\]
In the circuit considered, the value of total resistance is equal to sum of all the resistances.
i.e.,
\[{{R}_{eq}}={{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}\]
Current,
\[I=\frac{V}{{{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}}\]
The voltage across each resistor is given by the product of the voltage across that resistor and the current passing through it.
Voltage across resistor ‘Ra‘
\[{{V}_{{{R}_{a}}}}=I{{R}_{a}}\]
\[=\frac{V}{R}.{{R}_{a}}\text{ }\left[ I=\frac{V}{R} \right]\]
\[=\frac{V.{{R}_{a}}}{{{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}}\text{ }\left[ R={{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}} \right]\]
Similarly,
Voltage across resistor ‘Rb‘
\[{{V}_{{{R}_{b}}}}=\frac{V.{{R}_{b}}}{{{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}}\]
Voltage across resistor ‘Rc‘
\[{{V}_{{{R}_{C}}}}=\frac{V.{{R}_{b}}}{{{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}}\]
Voltage across resistor ‘Rd‘
\[{{V}_{{{R}_{d}}}}=\frac{V.{{R}_{d}}}{{{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}}\]
Voltage across resistor ‘Re‘
\[{{V}_{{{R}_{e}}}}=\frac{V.{{R}_{e}}}{{{R}_{a}}+{{R}_{b}}+{{R}_{c}}+{{R}_{d}}+{{R}_{e}}}\]