“Maximum power transfer theorem states that the maximum power can be transferred from source (voltage source, current source) to the load only when the load resistance (RL) is equal to the internal resistance of the source (Ri)”.
i.e,
\[{{R}_{L}}={{R}_{i}}\]
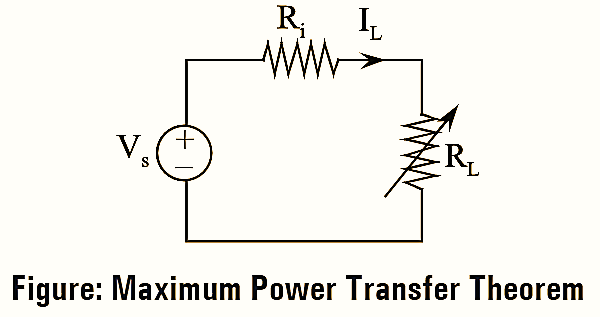
Maximum Power Transfer Theorem Explanation & Derivation
Consider a network consisting of voltage source (Vs), internal resistance (Ri) and variable load resistance (RL) connected in series as shown in figure.
Power across load is given by,
\[{{P}_{L}}=I_{L}^{2}{{R}_{L}}\]
From the figure,
Load current,
\[{{I}_{L}}=\frac{{{V}_{s}}}{\left( {{R}_{i}}+{{R}_{L}} \right)}\]
Substituting equation (2) in equation (1), we get,
\[{{P}_{L}}={{\left( \frac{{{V}_{s}}}{\left( {{R}_{i}}+{{R}_{L}} \right)} \right)}^{2}}{{R}_{L}}\]
\[{{P}_{L}}=\frac{V_{s}^{2}}{\left( {{R}_{i}}+{{R}_{L}} \right)}\times {{R}_{L}}\]
The condition for maximum power can be obtained by differentiating equation (3) with respect to load resistance, RL and equating it to zero.
i.e.
\[\frac{d{{P}_{L}}}{d{{R}_{L}}}=0\]
\[=\frac{d}{d{{R}_{L}}}\left[ \frac{V_{s}^{2}}{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{2}}} \right]=0\]
Applying \[\frac{U}{V}\] differentiation rule, we get,
\[\frac{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{2}}\times \frac{d}{d{{R}_{L}}}\left( V_{s}^{2}{{R}_{L}} \right)-\left( V_{s}^{2}{{R}_{L}} \right)\frac{d}{d{{R}_{L}}}\left[ {{\left( {{R}_{i}}+{{R}_{L}} \right)}^{2}} \right]}{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{4}}}=0\]
\[\frac{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{2}}\times V_{s}^{2}-\left( V_{s}^{2}{{R}_{L}} \right)\frac{d}{d{{R}_{L}}}\left[ \left( R_{i}^{2}+R_{L}^{2}+2{{R}_{i}}{{R}_{L}} \right) \right]}{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{4}}}=0\]
\[\frac{\left( R_{i}^{2}+R_{L}^{2}+2{{R}_{i}}{{R}_{L}} \right)V_{s}^{2}-\left( V_{s}^{2}{{R}_{L}} \right)\left( 0+2{{R}_{L}}+2{{R}_{i}} \right)}{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{4}}}=0\]
\[V_{s}^{2}\left[ R_{i}^{2}+2{{R}_{i}}{{R}_{L}}+R_{L}^{2}-2{{R}_{L}}\left( {{R}_{L}}+{{R}_{i}} \right) \right]=0\]
\[R_{i}^{2}+2{{R}_{i}}{{R}_{L}}+R_{L}^{2}-2{{R}_{L}}-2{{R}_{i}}{{R}_{L}}=0\]
\[R_{i}^{2}-R_{L}^{2}=0\]
\[R_{i}^{2}=R_{L}^{2}\]
\[{{R}_{i}}={{R}_{L}}…(1)\]
Hence, the maximum power will be transferred from source to the load when the internal resistance (Ri) of the source is equal to the load resistance (RL). Under this condition, the maximum power transferred to the load will be,
\[{{P}_{L\max }}=\frac{V_{s}^{2}}{{{\left( {{R}_{i}}+{{R}_{L}} \right)}^{2}}}\times {{R}_{L}}\]
\[=\frac{V_{s}^{2}}{{{\left( 2{{R}_{L}} \right)}^{2}}}\times {{R}_{L}}\text{ }\left[ \text{From the eqaution (1)} \right]\]
\[=\frac{V_{s}^{2}}{4{{R}_{L}}^{2}}\]
Maximum Power Transfer Theorem for AC Excitation
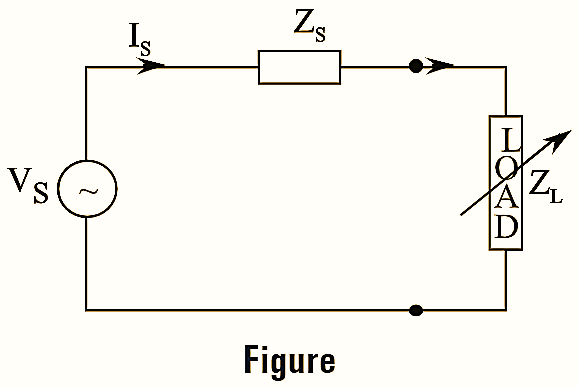
“Maximum power transfer theorem when applied to complex impedance circuits states that maximum power is transferred from source to load, when load impedance is equal to complex conjugate of source impedance”.
i.e,
\[{{Z}_{L}}=Z_{S}^{*}\]
Consider a network with complex load impedance ZL as shown in figure.
\[{{Z}_{S}}={{R}_{S}}+j{{X}_{s}}\]
\[{{Z}_{L}}={{R}_{L}}+j{{X}_{L}}\]
Current flowing through circuit,
\[{{I}_{L}}=\frac{{{V}_{S}}}{{{Z}_{S}}+{{Z}_{L}}}=\frac{{{V}_{S}}}{\left( {{R}_{S}}+j{{X}_{S}} \right)+\left( {{R}_{L}}+j{{X}_{L}} \right)}\]
\[=\frac{{{V}_{S}}}{\left( {{R}_{S}}+{{R}_{L}} \right)+j\left( {{X}_{L}}+{{X}_{L}} \right)}\]
Real power across load is given by,
\[{{P}_{L}}={{\left| {{I}_{L}} \right|}^{2}}{{R}_{L}}\]
\[{{P}_{L}}=\left| \frac{{{V}_{S}}}{\left( {{R}_{S}}+{{R}_{L}} \right)+j\left( {{X}_{L}}+{{X}_{L}} \right)} \right|\times {{R}_{L}}\]
Also
\[{{P}_{L}}=\frac{V_{S}^{2}{{R}_{L}}}{{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}+{{\left( {{X}_{L}}+{{X}_{L}} \right)}^{2}}}…(2)\]
Now by varying XL, the condition for maximum power flow is obtained. It is given as,
\[\frac{d{{P}_{L}}}{d{{R}_{L}}}=0\]
\[\frac{d}{d{{X}_{L}}}=\left[ \frac{V_{S}^{2}{{R}_{L}}}{{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}+{{\left( {{X}_{L}}+{{X}_{L}} \right)}^{2}}} \right]=0\]
\[V_{S}^{2}{{R}_{L}}\frac{d}{d{{X}_{L}}}\left( {{\left[ {{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}+{{\left( {{X}_{L}}+{{X}_{L}} \right)}^{2}} \right]}^{-1}} \right)=0\]
\[V_{S}^{2}{{R}_{L}}{{\left[ \left( -1 \right){{\left[ {{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}+{{\left( {{X}_{L}}+{{X}_{L}} \right)}^{2}} \right]}^{-1}} \right]}^{-1}}\frac{d}{d{{X}_{L}}}{{\left( {{X}_{L}}+{{X}_{L}} \right)}^{2}}\]
\[-V_{S}^{2}{{R}_{L}}\left[ {{\left[ {{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}+{{\left( {{X}_{L}}+{{X}_{L}} \right)}^{2}} \right]}^{-2}} \right]\times 2\left( {{X}_{L}}+{{X}_{L}} \right)=0\]
\[\frac{-V_{S}^{2}{{R}_{L}}\times 2\left( {{X}_{S}}+{{X}_{L}} \right)}{{{\left[ {{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}+{{\left( {{X}_{S}}+{{X}_{L}} \right)}^{2}} \right]}^{2}}}=0\]
\[2\left( {{X}_{S}}+{{X}_{L}} \right)=0\]
\[{{X}_{S}}+{{X}_{L}}=0\]
\[{{X}_{S}}=-{{X}_{L}}\]
Now substituting XS = -XL in equation (2), we get,
\[{{P}_{L}}=\frac{V_{S}^{2}{{R}_{L}}}{{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}}…(3)\]
The condition for maximum power can be obtained by differentiating equation (3) with respect to load impedance RL and equating it to zero.
i.e,
\[\frac{d{{P}_{L}}}{d{{R}_{L}}}=0\]
\[\frac{d}{d{{R}_{L}}}\left[ \frac{V_{S}^{2}{{R}_{L}}}{{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}} \right]=0\]
Applying differentiation rule, we get,
\[V_{S}^{2}\left[ \frac{{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}\times 1-{{R}_{L}}\times 2\left( {{R}_{S}}+{{R}_{L}} \right)}{{{\left[ {{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}} \right]}^{2}}} \right]=0\]
\[{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}-2{{R}_{L}}\left( {{R}_{S}}+{{R}_{L}} \right)=0\]
\[R_{S}^{2}+R_{L}^{2}+2{{R}_{S}}{{R}_{L}}-2{{R}_{L}}{{R}_{S}}-2R_{L}^{2}=0\]
\[R_{S}^{2}-R_{L}^{2}=0\]
\[R_{S}^{2}=R_{L}^{2}\]
Hence, maximum power transfer takes place when RS = RL and XS = -XL i.e., RS + jXS = RL + jXL. This means that maximum power will be transferred from source to load when the load impedance (4) is equal to conjugate of source impedance 4.
i.e,
\[{{Z}_{S}}=Z_{L}^{*}\]
Under this condition, maximum power transferred to the load will be,
\[{{P}_{L\max }}=\frac{V_{S}^{2}{{R}_{L}}}{{{\left( {{R}_{S}}+{{R}_{L}} \right)}^{2}}}\text{ }\left[ \text{From the eqaution (3)} \right]\]
\[=\frac{V_{S}^{2}{{R}_{L}}}{{{\left( 2{{R}_{L}} \right)}^{2}}}\]
\[{{P}_{L\max }}=\frac{V_{S}^{2}}{2{{R}_{L}}}\]